Page 174 - WCS - Electrical

WORKSHOP CALCULATION & SCIENCE - CITS

Force applied π 2 π
d =
Stress = 4 4
cross

sectional
Original
area

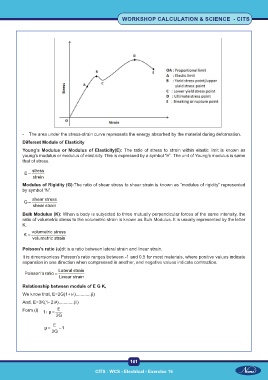
- The area under the stress-strain curve represents the energy absorbed by the material during deformation.
Force applied π 2 π
d =
Stress = Original cross sectional area Load 500 500
Different Module of Elasticity
4
4
=
N
σ = Stress = (or) forced = applied Stress = Area 2 16π = 16x 500
Load
22
π
π
Young’s Modulus or Modulus of Elasticity(E): The ratio of stress to strain within elastic limit is known as
Force
d =

Load
500
Area
2
7
4
4

Original
=
mm sectional s

=
cros
Stress =
area
N
forced
Load

(or)
young’s modulus or modulus of elasticity. This is expressed by a symbol “E”. The unit of Young’s modulus is same

22
16π
Area
σ = that of stress. = 16x
π
Area Force 2 applied Force applied 500x7 d = π 500 d = π
500
= Load
π 2
mm
7 2
Stress = Stress = Nsectional s area Stress = 16x22 4 = 16π 4 = 4 22 4
Load
stress forced (or) Original
cros

Area

cross
Original
π
σ = E = strein = = Force applied sectional area 500x7 π 2 16x 7
d =
Stress
=
Area
2
mm
stress Original cross sectional area 16x22 4 500 4 500 500 500
Load

Applied
load Load
= π

Modulus of Rigidity (G):The ratio of shear stress to shear strain is known as “modulus of rigidity” represented
=
E =
Stress = π 2 π
Force

applied
=
Stress =

Spring
=

applied
Force
stiffness = π 2
N
Lo
stress
Area d =
Load
G = Stress strein (or) ad = forced = (or) forced = area N 500x7d = 16π 500 22 16π 16x 22
shear =
Stress
Deflection Area
16x
Load 4
=
σ =
4

500
4
4
sectional

by symbol “N”. σ = cross Original
Original
sectional

Area

load
16x22 =
Stress
strain
Area
shear stress (or) cross mm 2 N area 2 Spring stiffness = Applied = = 7 22 7
forced
Load
E =

mm
Area
16π
10
σ
16x
shear = stress = Load 500 500
Deflection
strein
newtons 500x7 500Load

500
G = Area mm 2 600 Stress = = = 30 500x7 7
=
Stress =
=
=

shear
Applied
load
N
=
Loa

22
Load
(or)

N

mm = 16x22 16πArea
30
volumetric strain forced (or) d stress forced = stress Spring stiffness Area 16π 10 16x22 22
stress
σ
=
=
16x
σ =
500x7
K = shear = Area 2 600 newtons Deflection 16x 7
stress
E
E =
Area
Bulk Modulus (K): When a body is subjected to three mutually perpendicular forces of the same intensity, the
mm
7
2
=
G =
mm
volumetric
strain
strein
30
strein
16x22
shear

strain stress

mm

30
stress
stress
ratio of volumetric stress to the volumetric strain is known as Bulk Modulus. It is usually represented by the letter
Ultimate

volumetric
E =
Applied
500x7
K = Factor of Safety = 500x7 10 load Applied load
strein
=
Spring
stiffness
K. volumetric strain shear stress Spr 600 stiffness ing newtons = Deflection =
=
stress
Safe

stress

shear
16x22
30
G =
s
stress
UltimateA
ess =
G

volume E =
Poisson' K s = ratio = E = stres strain shear strain Factor of S 30 mm 16x22 = stress load pplied Deflection
Lateral str tric
shear

strain
Safety = stiffness pring
strein

shear
stressection
Safe
Defl
strain

Linear strain tric
volume G = strein stress Ultimate stress 10 10
load

stress = newtons 600
d
Applie
Safe
newtons
600 pplied
A
load
Poisson' s ratio = Lateralr strain strain Factor Spring stiffness = stress stress 30
shea
Ultimate

30
stiffness =
Spri
Safe
ng
of
Safety =

stress
shear
mm

Deflection
stress
stress
volumetric shear

30
mm
Linear
volumetric

stress
stress
Poisson’s ratio (u):It is a ratio between lateral strain and linear strain. 30 Ultimate Safe Deflection 10
600
stress
newtons

G =

strain
K = G
E =

K =
strain
strain
volumetric shear
μ =
1+
volumetric
strain
Poisson' s ratio shear strain stress strain Safe stress = Safe mm 30 Ultimate 10 30
Lateral
2.5
stress

10
volumetric
It is dimensionless Poisson’s ratio ranges between -1 and 0.5 for most materials, where positive values indicate

stress
2G =
=
K =
Ultimate
600
newtons

of 6
newt
Safety =ons 00
Factor

E Linear

strain
Ultimate of actor
stress =
F
Safety

4
expansion in one direction when compressed in another, and negative values indicate contraction. stress

volumetric
strain
30
stress 30
Safe

Safe
1+ μ = 1 2G volumetric stress Safe stress = 30 mm stress stress stress
2.5 mm 30
E

Ultimate
volumetric

stress
Safe
μ = K = − Lateral strain Lateral strain Fac = tor of Safety =
K =
Ultimate

stress
2G
s volumetric
Poisson' v ratio = strain Safe stress = 4 Safe stress
E Poisson' strain olumetric

s
ratio =
Ultimate
1+ μ E = − 2G 1 Linear strain strain strain Factor 2.5 of Safe stress = stress stress
stress
te

Ultima

Ultimate
Linear
Ultimate
stress
Factor
safety

Lateral
μ =
o
Factor
Safe
stress =y f
Safet =
= Safety of

=
Ultimate
stress
s
Poisson'
ratio =
2G
stress
stress
Safe
2.5ss

Linear
strain

Relationship between module of E G K, Safe stre π = 4 2 Safe Sa fe stress Safe stress
Ultimate

stress
(4.2) Factor
safety
of
Lateral

strain
 E
E
  E E   − E  Lateral strain = 4 × Safe stress =
4

Po
μ = 1+ sisson'
stress
μ
Safe
1 = ratio =
−1
1
  ratio s
 Poisson'
= 3K=
 −1+

μ
+ 2 =
 − 21We know that, E=2G(1+ )............(i) π Ultimate stress 2.5
2.5

2G

 2G
strain
Linear
2 Ultimate

G
 2Gin

stress = =
  2G    Linear stra Safe 2.5 × stress fe (4.2) = Ultimat = stress e stress
E
= Sa
stress

 And, E=3K(1- 2 )............(ii)   − E + 2  2.5 Safe 4 Factor 4 = of safety 4
 E
  μ =+
1
4
2.5 Safe

stress

Safe
stress
 − 21
−1
1

  E
= 3K 2G

E

=

22
1
 2G μ =
π
 
 μ =
Form (i)
−

E
4.2× 2

E
Ultimate

Ultimate
×
=
μ
1+
μ =
stre
Sa
 
 E
    E 1+ 2G = −  3G  - E G 2G  1 = 4 fe × 2.5 7×ss × (4.2) 4.2 4 stress stress
4 = 2.5
E
Safe

stress =

E
 
4 2.5
4
=
= 3K   = 2G
3K − 21  −3    −1μ  2G  −  + 2  2.5 22 Factor of safety of safety
1

 = 3K 1−
=
Factor

 
30×4.2.2× Ultimate

stress
×
Load 4× 4
G
4
    2G      2G G   G  Working = Safe stress = 1000
×
E
  E   E  3G - E  stress = 74 2.5 4 = π Fa 2 2.5 of ctor π safety
600
1
3K   −3  μ =   μ =  E = 3K − −  1    2.5 = Area × (4.2) = × (4.2) 2

stress
22 4 Ultimate

G  E

  
100044 stress e
4
2G
Load Ultimat
E  
30×
−1
= Safe
× stress

    − 21 G   2G  = 3K 1  − −1 + 2  = 3K   − E + 2   Working Safe stress = × = 4.2× π 4.2 2
stress = 2.5
  − 2
1
  1
 

=
Ultimate ×=
E    9KG 2G        E    3G  2G  G    E   G  4 7× 4 Fa (4.2)safetyc stress of tor
600 safety of r
AreaFacto



E
E
  
=

-  
4
3K  G  −1      = 3K  −1   =  3K  − + 2  Factor of safety = Working 4
 −3
1
+ 3K2
stress


G
2

2.5 2.5
30× 2
   9KG     2G  G      G  stress = Load π.5 × 22 π = (4.2) 2 1000

=
(4.2)
stress 222.5
Ultimate
= =
4.2
E =     E       E   Working safety =Area44 × × × = 4.2× × × 4.2× 4.2
E
 E
Factor

of
600
4 4
 − 21
+ 2
7×
1
−1
 3G  −

- 1
stress 7×
 −1  G         = 3K1     = 3K  − E + 2    3G - E  4 4 Working 4 4
+ 3K E − 2
E
22
2.5

  

3K  2G
  
 −3 2G
G
 
 3K
 = 3K 

   9KG G   = 3K   −3   G G    450 M.Pa Load stress 100030× 4.2
×
×
 
=
4.2×


=
Ultimate

 

4

 
E  =          G  3G - E   G  161 Factor of ng 50y M.Pa = 4 7× stress = Load = 30× 1000
E
safet
=
=
Worki
stress
Working

22
2.5
 G 3K  −    = 3K   450 ×= M.Pa × stress 600 Area 600
+ 3K 3
Working
Area
2.5
22

Load 4.24.2×

=
×
30×



=
7×
4
4
      9KG   G    3G - - E G   CITS : WCS - Electrical - Exercise 16 stress Working 4 M.Pa = 4 × 4.2× = 4.2 1000
7×
E
 
E
50
E
 3G
Area
 = 3K
3K


Ultimate
3K  −3 G   = 3K  9KG     Factor of safety = Ultimate stress 600 stress
  −3
E

  

=
=

 E
M.Pa of


+ 3K  
Load
30×
G
  
     G G  9KG    G G    Workin 450 Factor Load safety = 100030× 1000 stress
+ 3K
stress

Working
=
= stress g
=

Working
Working
stress =
=


600
Area
600
E =  + 3K  Factor 50 M.PaArea Ultimate stress

of
safety =
 G
Working

stress
 9KG    450 Ultimate stress
 9KG
stress
Ultimate
M.Pa
E
of
Factor
= safety =
=
E =     Factor of safety = 450 M.Pa
=
+ 3K
 G
Working
M.Pa

 G + 3K   50 450 M.Pa 50 stress
stress
Working
M.Pa
= 50 M.Pa
450
450 M.Pa
M.Pa
=
= 50 M.Pa
50
M.Pa