Page 42 - CITS - WCS - Mechanical

WORKSHOP CALCULATION - CITS

Trigonometric Formula Ratios In Other Words
Trigonometry ratios relate angles and sides in triangles in Trigonometry. Sine (sin) is opposite/hypotenuse, cosine
(cos) is adjacent/hypotenuse, and tangent (tan) is opposite/adjacent. These trigonometric ratios help us to solve
triangle problems and model world phenomena in various fields, like physics, space, and engineering.
Sinθ = Opposite Side / Hypotenuse
cosθ = Adjacent Side / Hypotenuse
tanθ = Opposite Side / Adjacent Side
secθ = Hypotenuse / Adjacent Side
cosecθ = Hypotenuse / Opposite Side
cotθ = Adjacent Side / Opposite Side.
Trigonometry Formulas in Degrees
Trigonometry ratios are used to create the relationship between triangle angles and side lengths. The identities
and ratios serve as the foundation for all trigonometry formulas. Trigonometry formulas are displaying common
trigonometric functions for angles in degrees. This is made up of trigonometric ratios such as sine, cosine,
tangent, cosecant, secant, and cotangent. These ratios can be expressed as sin, cos, tan, cosec, sec, and cot
in a trigonometry table. The trigonometric ratios values can be used to calculate the values of trigonometric
standard angles such as 0°, 30°, 45°, 60°, and 90°.

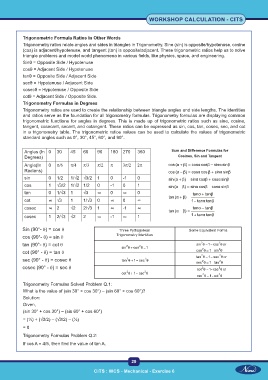
Angles (In 0 30 45 60 90 180 270 360 Sum and Difference Formulas for
Degrees) Cosines, Sin and Tangent
Angle(In 0 π/6 π/4 π/3 π/2 π 3π/2 2π cos (α β) cosα cosβ sinα sinβ
Radians) cos (α β) cosα cos β sinα sinβ
sin 0 1/2 1/√2 √3/2 1 0 -1 0 sin (α β) sinα cosβ cosα sinβ
cos 1 √3/2 1/√2 1/2 0 -1 0 1 sin (α β) sinα cosβ cosα sinβ
tan 0 1/√3 1 √3 ∞ 0 ∞ 0 tanα tanβ

cot ∞ √3 1 1/√3 0 ∞ 0 ∞ tan (α β) 1 tanα tanβ
cosec ∞ 2 √2 2/√3 1 ∞ -1 ∞ tan (α β) tanα tanβ
cosec 1 2/√3 √2 2 ∞ -1 ∞ 1 1 tanα tanβ

Sin (90°- q) = cos q Three Pythagorean Some Equivalent Forms
2
2
2θ
cos
2 or θ
1
sin
1
cos
sin
cos (90°- q) = sin q Trigonometry Identities sin 2 θ 1 cos 2 θ or sin 2 θ 1 cos 2 or θ
2 θ
2 or θ
2 or θ
2θ
sin 2 2 θ 1 cos 2 2 or θ sin 2 1 cos 2
cos
1
cos 2θsin
2 or θ
2θ 1θ
sin 2
θ θ
tan (90°- q) = cot q 2 2 cos 2 θ 2θsin 1 sin co 2 θ 2θs 2 1 sin 2 2 θ 1 sin1 cos 2 2 θ θ θ or
cos
2
sin
1
cos
sin θ cos θ 1 sin 2 θ sin 1 θ cos co co 2 or θ θs 2 1 1 cos 2 2θ 1 sin 2θ 2
2
2 θ 2 θs

sin
1
sin
1 sec
tan
sin
cot (90° - q) = tan q sin 2 2 θ cos 2 sec 2 1 θ cos 2 θ 2 θsin 1 2θ sec cos 1 cos 2θ 2θsec 2 1 1 θ cos2 2θ 1θ 1 sec 2θ 2 or θ
2
tan
2θ 1
cos 2 θtan
1 sec
θ or θ
θ 1
sin 2
tan
θ
tan
θ 2θsin 2 θtan
2 or θ
θ 2 se
or 1θ 2 θc
θ
2
1
2 θ
tan
2
sin co
cos tan
1 1θ
2θ
2
sec 2θtan
sec (90° - q) = cosec q sin 2 2 θ cos csc 2 θ tan 2 θ θsin 2 2 θ 1 tan 1 1 1 2 θ θssec 2 2 2θ θ tan 2 θ 1 sec 2 2 or θ θ θ or
2 or θ
1
sec
θ
2 θ 2θtan 2θcot
2 or θ sec 2θcsc
2θ 1θ
sec 1 1
1
2 1
tan 2
2θ
sec
1
tan
2 θ
tan 2 θsec
1 tan1
θ sec 2 θcsc
1 θ
sec cot
cot
θ
sec 2
θ
1
θ 2θtan 2
2 θ
2 θ
tan
2 tan 2 θcot
1
2 sec 2 θcsc
sec
2θ
2 θ cot
2
sec 1
sec
cosec (90° - q) = sec q tan 2 2 θ 1 csc 2 θ tan 2 θ 2θcot 1 - 1 θ csc 1 tan 1 2 θ csc 2 or θ csc 2θ θ sec2 2θ 1 tan 2 2θ θor θ
sec
θ
2θor θ
2θ 1θ
θ
1
cot
2θ
1
1 csc-
cot
sec2
tan 2
1 csc-
θ 1
sec 2 θcot
θ
θ cot
cot
or csc
tan 2
2
2
2 or θ
cot 2 θ 1 csc 2 θ sec 2 θ 1 tan 2 θ cot 2 θ - 1 - 1 csc 2 or θ
2θ
csc 2
cot 2
csc
cot 2 θ - 1 csc 2 or θ cot 2 - 1 - csc 2θcot 2 or θ
2θ 1θ
θ
csc 2 θ - 1 cot 2 θ cot 2 θcsc 2 θ - 1 cot- 1 - 1 csc 2 2 θ θ θ or
csc
cot
csc
csc
θ
Trigonometry Formulas Solved Problem Q.1: cot 2 θ - 1 - 1 csc 2 or θ θ csc 2θ - 1 - 1 - 1 cot 2θ θ
cot
cot
2θ
2θ
cot
csc
θ
What is the value of (sin 30° + cos 30°) – (sin 60° + cos 60°)? csc 2 θ - 1 cot 2 θ
Solution:
Given,
(sin 30° + cos 30°) – (sin 60° + cos 60°)
= (½) + (√3/2) – (√3/2) – (½)
= 0
Trigonometry Formulas Problem Q.2:
If cos A = 4/5, then find the value of tan A.
29
CITS : WCS - Mechanical - Exercise 6 CITS : WCS - Mechanical - Exercise 6