Page 44 - CITS - WCS - Mechanical

WORKSHOP CALCULATION - CITS

EXERCISE 7 : Graphs

Basic Concept:
A basic two-dimensional graph contains of a vertical and a horizontal line which is intersects at a point called
origin. The horizontal line is the x axis, the vertical line is the y axis. In simple line graphs, the x and y axes are
each divided into similarly spaced subdivisions that are assigned to numerical values. A graph is determined
as a structure of mathematical which is represents a particular function by connecting a set of points. It is used
to generate a pair wise relationship between objects. Graph is mathematic representation of a network and it
describes the relationship between lines and points.

Importance

Graphs play an essential role in our everyday lives, often going unnoticed as powerful tools that bring information
in a visual and accessible manner. Whether in education, business, or personal decision-making, graphs help us
make sense of complex data and also tell compelling stories. The three superiorities of graphs are as follows: it
makes data presentable and easy to understand. It helps in summarizing the data in a crisp manner. It helps in
the comparison of data in a stronger way. Modern Applications of Graph Theory discusses many cutting-edge
applications of graph theory, such as traffic networks, navigable networks and optimal routing for emergency
response, and graph-theoretic approaches to molecular epidemiology.
Plotting Graphs of Simple Linear Equation
In graphs there are three basic procedure of graphing linear functions. The first is by plotting points and then
drawing a line through the points. The second is by using the y-intercept and slope. And the third is by using
transformations of the identity function f(x)=x.
Graph Linear Equations in Two Variables
• Plot points in a rectangular coordinate system.
• Graph a linear equation by plotting points.
• Graph vertical and horizontal lines.
• Find the x- and y-intercepts.
• Graph a line using the intercepts.

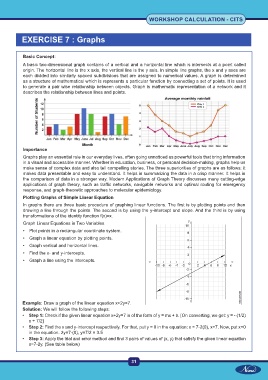
Example: Draw a graph of the linear equation x+2y=7.
Solution: We will follow the following steps:
• Step 1: Check if the given linear equation x+2y=7 is of the form of y = mx + b. [On converting, we get: y = - (1/2)
x + 7/2]
• Step 2: Find the x and y-intercept respectively. For that, put y = 0 in the equation: x = 7-2(0), x=7. Now, put x=0
in the equation. 2y=7-(0), y=7/2 = 3.5
• Step 3: Apply the trial and error method and find 3 pairs of values of (x, y) that satisfy the given linear equation
x=7-2y. (See table below)

31

CITS : WCS - Mechanical - Exercise 6